Exemples d'algorithmes
Date de publication : 05/03/2005 ,
Date de mise a jour : 05/03/2005
Par
Selkis (selkis.developpez.com)
Dans le cours qui va suivre, nous allons utiliser un pseudo-langage, comportant toutes les structures de base d'un langage de programmation.
I. Rechercher une symétrie dans une chaine de caractères
II. Compter une lettre dans une phrase
III. Savoir si une année est bissextile ou pas
IV. Les tris
IV.1. Le tri à bulles
IV.2. Le tri par sélection
IV.3. Le tri par Permutation
IV.4. Le tri par comptage
V. Factorielle, recursivité et répétitive
VI. Recherche Dichotomique
I. Rechercher une symétrie dans une chaine de caractères
Un palindrome est une chaîne de caractères que l'on peut lire identiquement de droite à gauche, et de gauche à droite.
Par exemple :
AA.
38783.
LAVAL A ETE A LAVAL.
Soit une chaîne de caractères terminée par un point.
Nous allons ecrire 'algorithme d'un programme permettant d'affirmer si cette phrase est ou non un palindrome.
Jeu d'essai
'.' c'est un palindrome
'a.' c'est un palindrome
'aba' c'est un palindrome
'acb.' ce n'est pas un palindrome
'aacba.' ce n'est pas un palindrome
'aacab.' ce n'est pas un palindrome
Constantes
charterm = "." //caractère marquant la fin de la chaîne
taille = 80 //nbr maximum de caractère dans la chaîne
Types chaîne = tableau[taille]de caractères //type des chaînes de caractères traitées
Variables phrase : chaine //phrase dans laquelle on va déterminer la symétrie
i : entier //indice de parcours de la phrase par le debut
j : entier //indice de parcours de la phrase par la fin
Début Programme //saisie de la phrase
Ecrire ('donnez une phrase terminée par un carctère ',carterm)
Lire (phrase) //calcul de la longueur de la phrase
j : = 1;
Tantque (phrase[j]<>charterm) faire //arrêt sur le charactère de terminaison
j := j + 1
Fintantque
j := j -1 //Parcours de la phrase par les 2 bouts pour ne pas ..
i := 1 //..compter le caractère de terminaison
Tantque (i < j) et (phrase[i]=phrase[j]) faire //arrêt quand les indices se croisent ou quand il n'y a pas de symétrie
i:= i +1
j := j -1
Fintantque//fin du parcours, il y a symétrie
Si i>=j alors //affichage du résultat
Ecrire ('c'est un palindrome')
sinon
Ecrire ('ce n'est pas un palindrome')
Fsi
Fin Programme
II. Compter une lettre dans une phrase
Soit une chaîne de caractères terminée par le caractère "." ,
Nous allons donner l'algorithme d'un programme qui compte le nombre d'occurences d'une lettre donnée ('a' par exemple).
Création du jeu d'essai
1) Pas de lettre
lettre 'a'
Terminateur "."
Phrase "."
résultat 0
2) Pas de bonne lettre
lettre 'a'
Terminateur "."
Phrase "etoiles."
résultat 0
3) Que des bonnes lettres
lettre 'a'
Terminateur "."
Phrase "aaaaaa."
résultat 6
4) Mixtes
lettre 'a'
Terminateur "."
Phrase " mon chat est amusant."
résultat 3
4) La lettre recherchée est le terminateur
lettre '.'
Terminateur "."
Phrase "mon chien est gentil."
résultat 0
nb : le terminateur ne fait pas partie des caractères à traiter, il est juste présent,
nous nous en occuperons donc pas dans le cadre de cet algorithme.
Programme compter_une_lettre
Constantes charfind = 'a' // caractère dont les occurences sont comptées.
charfin = "." //caractère de fin de chaîne.
taille = 80 //nbr maximum de caractère dans la chaîne
Types chaîne=tableau[taille]de caractères //type des chaînes de caractères traitées
Variables phrase : chaine //phrase dans laquelle les charfind sont comptés
i : entier //indice de parcours de la phrase
compteur : entier //compteur des charfind dans la phrase
Début //initialisation des compteurs et lecture de la phrase
Ecrire('donnez une phrase terminée par un carctère ',charfin)
Lire(phrase)
i : = 1
compteur=0
//Parcours de la phrase avec recherche des carctères charfind
//Il y a 0 ou plusieurs caractère à parcourir
Tantque (phrase[i]<>charfin) faire //arrêt sur le charactère de fin
Si phrase[i]=charfind Alors
compteur : = compteur + 1 //1 caractère recherché trouvé
Finsi
i : = 1+ 1 //on passe au caractère suivant
Fintantque
Ecrire('le nombre de caractères ',charfin,' dans la phrase est de : ', compteur) //résultat du parcours
Fin
III. Savoir si une année est bissextile ou pas
En fait c'est trés simple,
si l 'année est divisible par 4 et quand même temps elle n'est pas divisible par 100 ou au contraire qu'elle soit divisible par 400 alors elle est bissextile, sinon elle ne l'est pas.
Algorithme de principe Entier annee
Debut Programme
Ecrire "Veuillez saisir l'année"
lire annee
si (annee mod 4=0) et ((annee mod 100>0) ou (A mod 400=0)) alors
Ecrire "L'année ", annee, "est bissextile."
sinon
Ecrire "L'année ", annee, "n'est pas bissextile."
fin de si
fin Programme
IV. Les tris
IV.1. Le tri à bulles
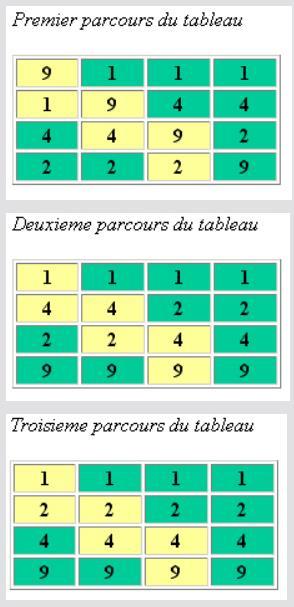
Plus astucieux que le tri_par selection, le principe du tri à bulle est de faire remonter petit a petit un élément trop grand vers le haut du tableau en comparant les éléments 2 a 2.
Si l 'élément de gauche est supérieur à son voisin de droite on les inverse et on continue avec le suivant.
Lorsque l'on est en haut du tableau on repart au début et on s'arrête lorsque tout les élements sont bien placés.
| J.Essai 1 |
taille = 0 |
éléments du tableau : 4 1 3 9 6 8 7 0 5 2 |
| J.Essai 2 |
taille = 1 |
éléments du tableau : 0 4 3 1 2 8 5 6 7 9 |
| J.Essai 3 |
taille = 10 |
éléments du tableau : 2 3 4 5 1 6 7 8 9 0 |
Principe (tableau (4)= 9 1 4 2 )
Algorithme ' i: entier // indice de parcours de la table d'entiers
' inversion : booléen //vrai quand il y a eu au moins 1 inversion
' tampon : entier : variable intermédiare permetttant l'inversion de 2 entier du tableau
faire
inversion = faux
Pour i allant de 0 a FinTableau -1
// comparaison de l'élément en cours à son suivant
Si tableau(i) > tableau(i + 1) alors
// il faut inverser les deux éléments tableau
tampon = Tableau(i)
Tableau(i) = Tableau(i + 1)
Tableau(i + 1) = tampon
//il y a eu au moins une inversion
inversion = vrai
Fin de si
Fin de pour
Jusqu 'à (inversion=faux)
 |
Optimisation de l'algorithme
|
Cette version du tri à remontée des bulles arrête de trier le tableau quand i ne reste plus de nombre à trier.
L'emplacement de dernière inversion donne la longueur utile pour le prochain parcours.
' i: entier // indice de parcours de la table d'entiers
' der_inversion : entier //indique l'endroit de la dernière inversion ou 0
' tampon : entier : //variable intermédiare permetttant l'inversion de 2 entier du tableau
tant que fintableau >1 faire
der_inversion : = 0
i : = 1 // début du nouveau parcours
Répéter
// comparaison de l'élément en cours à son suivant
Si tableau(i) > tableau(i + 1) alors
// il faut inverser les deux éléments tableau
tampon = Tableau(i)
Tableau(i) = Tableau(i + 1)
Tableau(i + 1) = tampon
//il y a eu au moins une inversion
der_inversion : = 1 // note l'emplacement de la dernière inversion
Fin de si
i : = i + 1 //passage à l'élément suivant
jusqu'à i = fintableau //arrêt sur le dernier élément
fintableau : = der_inversion // le prochain parcours ne triera pa la fin du tableau (déja trié)
Fin tant que
IV.2. Le tri par sélection
Dans cet algorithme nous allons travailler sur un tableau de 10 entier.
Jeu d'essai
| 52 |
10 |
1 |
25 |
62 |
3 |
8 |
55 |
3 |
22 |
Principe :
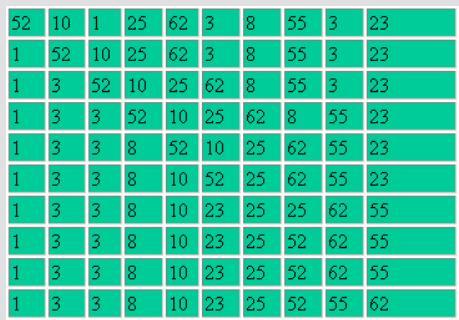
Le tri par sélection consiste à chercher le plus petit élément du tableau pour le placer en 1er, puis de chercher le plus petit élement dans le reste et de le mettre en second, etc…
On stock dans la variable petit le 1er élément du tableau puis on reparcour le tableau en partant de l'indice en cours jusqu'à la fin pour chercher si un élement est plus petit que lui.
Si c'est le cas on va remplacer la valeur de la variable petit par la nouvelle valeur trouvé puis stocker dans la variable position à quelle position du tableau on l'a trouvé .
La deuxieme boucle va nous permettre de mettre le plus petit élément trouvé à la bonne place et de décaler les autres élement.
Algorithme Pour i allant de 1 à (findutableau) -1 faire
Petit = tableau(i)
Pour j allant de i à (findutableau) faire
Si tableau(j) < petit alors
Petit = tableau(j)
Position=J
Fsi
Fin de pour
Pour j allant de position à ( i + 1) pas -1
tableau(j) = tableau(j - 1)
Fin de pour
Tableau(i)=petit
Prochain i
IV.3. Le tri par Permutation
Le tri par permutation est le tri du jeu de cartes.
Principe:
On parcourt le tableau jusqu'à ce que l'on trouve un élément plus petit que le précedent donc mal placé.
On prend cet élément et on le range à sa place dans le tableau puis on continue la lecture.
On s'arrête à la fin du tableau.
| Jeu d'essai |
52 |
10 |
1 |
25 |
62 |
3 |
8 |
55 |
3 |
23 |
| 1ere boucle |
10 |
52 |
1 |
25 |
62 |
3 |
8 |
55 |
3 |
23 |
| 2ieme boucle |
1 |
10 |
52 |
25 |
62 |
3 |
8 |
55 |
3 |
23 |
| 3ieme boucle |
1 |
10 |
25 |
52 |
62 |
3 |
8 |
55 |
3 |
23 |
| 4ieme boucle |
1 |
3 |
10 |
25 |
52 |
62 |
8 |
55 |
3 |
23 |
| 5ieme boucle |
1 |
3 |
8 |
10 |
25 |
52 |
62 |
55 |
3 |
23 |
| 6ieme boucle |
1 |
3 |
8 |
10 |
25 |
52 |
55 |
62 |
3 |
23 |
| 7ieme boucle |
1 |
3 |
3 |
8 |
10 |
25 |
52 |
55 |
62 |
23 |
| 8ieme boucle |
1 |
3 |
3 |
8 |
10 |
23 |
25 |
52 |
55 |
62 |
Algorithme i,j,k,permute : entier
POUR i ALLANT DE 1 A 9
FAIRE
SI(TAB(i+1)<TAB(i)) ALORS
permute <--TAB(i+1);
j<--1;
TANTQUE ((j<i) ET (TAB(j)<TAB(i+1)))
FAIRE j<--j+1
FTQ
POUR k ALLANT DE i+1 A j+1 PAS -1
FAIRE
TAB(k)<--TAB(k-1)
FIN POUR
TAB(j)<--permute;
FSI
FINPOUR
IV.4. Le tri par comptage
le tri par comptage consiste pour chaque élément du tableau à compter combien d'élément
sont plus petit que lui, grâce à ce chiffre on connaît la position dans le tableau résultat.
| Jeu d'essai |
52 |
10 |
1 |
25 |
62 |
3 |
8 |
55 |
3 |
23 |
| Nombre tableau [nb] |
7 |
4 |
0 |
6 |
9 |
1 |
3 |
8 |
1 |
5 |
| Position |
8 |
5 |
1 |
7 |
10 |
2 |
4 |
9 |
3 |
6 |
| Resultat |
1 |
3 |
3 |
8 |
10 |
23 |
25 |
52 |
55 |
62 |
 |
Le tableau [nb] contient le nombre d'element plus petit que celui passé en index
Position est egal au nombre d'element plus petit que celui passé en parametre + 1 (+ 2 pour le cas des doubles)
|
Algorithme Pour i allant de 1 a (fin de tableau)
Res(i) = 0
Nb(i) = 0
'calcule des compteurs
Pour j allant de 1 a (fin de tableau)
Si tableau(j) < tableau(i) alors
Nb(i) = nb(i) + 1
Fin de si
Fin de pour
Fin de pour
Pour i allant de 1 a (fin de tableau)
j = nb(i)
Tant que res(j) <> 0 'cas des doubles
j = j + 1
Fin de tant que
Res(j) = tableau(i)
Fin de pour
V. Factorielle, recursivité et répétitive
Le principe de la fonction factorielle et de multiplier un chiffre donnée (nb_donnée) par tous ses inférieurs.
exemple factorielle(4) = 4 * 3 * 2 * 1 = 24.
pour faire ce genre de calcul en informatique on fait appelle en général à une fonction récursive...
Une fonction récursive est une fonction qui s'appelle d'elle même, phénomène infini dont la question essentielle est de trouver la condition d'arrêt. (ici nb_donnée).
EXEMPLE RECURSIF Factorielle(nb_donnée)
si nb_donnée=1 alors
factorielle(1)=1
sinon
factorielle=nb_donnée * factorielle (nb_donnée-1)
fin si
fin fonction
Pour mieux comprendre imaginer une tele qui transmet une image dans laquelle il y a une tele qui transmet une image..et ainsi de suite , ou un miroir refletant un miroir refletant lui même un autre miroir et ainsi de suite..
Une fonction récursive peut etre transformée en répétitive chaque fois que la recursivité est terminale.
Une fonction est dite terminale lorsque dans le bloc de la fonction ou de la procédre, il n'y a pas d'instructions qui suivent l'appel récursif comme c'est le cas dans l'exemple recursif.
EXEMPLE REPETITIF factorielle(nb_donnée)
résultat =1
pour k=1 à nb_donnée
résultat=résultat * k
next k
factorielle= résultat
fin fonction
VI. Recherche Dichotomique
Soit une table contenant des prénoms, classés par ordre alphabétique, nous désirons chercher l'indice de la case du tableau ou se trouve un prénom dans ce dit tableau ,si il s'y trouve.
Le principe est assez simple....
On va commencer par lire le tableau, le prénom à rechercher, stocker la valeur 1 dans la variable inférieur et la longueur du tableau dans la variable supérieur.
Ensuite on va déterminer le milieu du tableau et initialisé la valeur trouve a faux.
Il nous reste plus qu'a écrire la boucle qui va nous permettre de trouver notre élément
La boucle consiste a délimiter le tableau et a le redimensionner de plus en plus petit a chaque fois que l'on fait un tour de boucle .
La première fois on se positionne sur le milieu du tableau et on regarde le prénom, si c'est le bon c'est du bol trouvé du premier coup , sinon on regarde si notre prénom est plus grand ou plus petit.
Si il est plus grand alors on va lui dire que la nouvelle borne de départ est le milieu du tableau + 1 élément pour pouvoir se positionner sur le prochain.
Si il est plus petit alors c'est l'inverse , c'est notre borne de fin qui va changer, elle va remonter jusqu'au milieu du tableau -1 cette fois.
Puis on remonte, comparer notre condition : est-ce que ma borne de fin est toujours plus grande que le debut
DEBUT PROGRAMME
LIRE tableau
LIRE prenom
inferieur =1
superieur = longueur du tableau
Tant que superieur >inferieur ET trouve <> 0 faire
milieu = PartieEntiere (inferieur + superieur) / 2
Si prenom(milieu) <> prenom alors
Si prenom > prenom(milieu) alors
Inferieur=milieu + 1
Sinon
Superieur=milieu - 1
Fin si
Sinon
Trouvé=milieu
Fin de si
Fin de tant que
FIN PROGRAMME
|
